Humans are obsessed with truth. We spend our lifetimes wandering about, seeking the truth. Aaaah… the objective truth… It is as if we don’t live our lives through our perception, our subjective experiences. We like to act like there is a transcendental truth somewhere out there, and our mission is to find it. We tend to just forget about our flawed perception and the great impacts of the process of evolution on us—on our thinking, our acts, our beliefs, our everything. Then the people of the Earth form the view of rigorous scientific disciplines, such as Mathematics, to state the absolute truth in its axioms. When science fails to predict or mispredicts something, science-haters and/or some religious people love mocking the scientists for “wasting their whole life on something that is clearly NOT TRUE”. Aah, these poor people…
“Dude, did you see how the professor used the axiom of choice to prove the theorem in the class? That made no sense…” “I know, dude. We cannot even pick elements from the infinite number of sets. Math is nonsense at this point…” The truth in the scientific discipline of mathematics is not in its axioms; it is in its implications. Mathematics is not concerned with the truth of its axioms, but the consistency of their implications. If the set of axioms implies ![]() and
and ![]() at the same time, then mathematicians shiver in fear. Otherwise, there is no issue even if one of the axioms may state that humans have 3 legs. Let me explain what I mean by giving a few examples.
at the same time, then mathematicians shiver in fear. Otherwise, there is no issue even if one of the axioms may state that humans have 3 legs. Let me explain what I mean by giving a few examples.
Note: The math presented in this post is not rigorous and is for the purpose of illustrating the essence of the mathematical coherence.
Examples of Mathematical Consistency
Mathematics is the language of rigor, and the grammatical reach of a language is what determines the boundaries of one’s imagination, speaking the language. The language does not need to be textual all the time. It can be visual, auditory, or even sensational. Mathematics is a symbolic language with a certain grammar. Within this grammar, we can construct new sentences that have never been constructed before. However, interpreting some of these constructions may not be easy or even impossible for us. We can do the same by using the natural languages that humans use to communicate with each other in everyday life. For example, the sentences “An apple has driven so fast through the table” or “A picture draws an artist” are syntactically correct, yet semantically meaningless. However, we can imagine what these sentences mean in an imaginary world just because we are able to construct them in the first place. For the first sentence, imagine an imaginary apple with four wheels going through a table, and for the second sentence, imagine a frame with hands holding a brush and drawing a person on a blank paper. None of these are real for us, and that’s the point of imagination. We can imagine because it is possible to construct syntactically, not because it makes sense semantically. However, sometimes seemingly nonsensical constructions may have an actual meaning in reality. Think about the following sentence as an example: The clock whispers secrets to the shadows, but only the moonlight listens.
From natural numbers to reals
It is intuitive enough for many people to grasp the idea of natural numbers. They are for, well, counting things. The process is very natural—you start from nothing and add one thing to it to get one, you then add one to that one thing to get two things, and so on. Have you ever wondered where the heck in this process do we get to the negative integers? ![]() may be used to represent 5 apples, 5 chairs, 5 hats, or 5 whatever. What on Earth does
may be used to represent 5 apples, 5 chairs, 5 hats, or 5 whatever. What on Earth does ![]() represent then? Well, the additional sign bit in front of the number can be used to represent two opposite actions on the specified number of things. For example,
represent then? Well, the additional sign bit in front of the number can be used to represent two opposite actions on the specified number of things. For example, ![]() could mean I am in possession of 5 dollars, and
could mean I am in possession of 5 dollars, and ![]() could mean I am in debt of 5 dollars. Moreover, the binary operations can have their own meanings when applied to two numbers:
could mean I am in debt of 5 dollars. Moreover, the binary operations can have their own meanings when applied to two numbers: ![]() can be used to denote the verb “to bring” and
can be used to denote the verb “to bring” and ![]() can be used to denote the verb “to take”. Then follows the logical rules of addition:
can be used to denote the verb “to take”. Then follows the logical rules of addition:
- A positive integer
 added to another positive integer
added to another positive integer 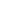 is the same as natural addition and hence,
is the same as natural addition and hence, 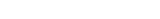 .
. - A positive integer
 added to another negative integer
added to another negative integer 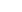 means the debt of
means the debt of 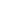 dollars is brought while in possession of
dollars is brought while in possession of 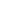 dollars. This is the same as saying
dollars. This is the same as saying 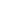 dollars are to be taken away while in possession of
dollars are to be taken away while in possession of 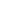 dollars and, hence,
dollars and, hence, 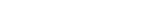 .
. - A negative integer
 added to another positive integer
added to another positive integer 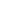 means the possession/fortune of
means the possession/fortune of 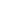 dollars is brought while in debt of
dollars is brought while in debt of 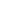 dollars. This is the same as saying taking away
dollars. This is the same as saying taking away 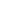 dollars while in possession of
dollars while in possession of 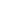 dollars and, hence,
dollars and, hence, 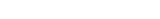 .
. - A negative integer
 added to another negative integer
added to another negative integer 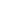 means the debt of
means the debt of 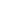 dollars is brought while in debt of
dollars is brought while in debt of 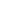 dollars. This is the same as saying taking away
dollars. This is the same as saying taking away 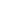 dollars while in debt of
dollars while in debt of 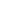 dollars and, hence,
dollars and, hence, 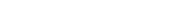 . Moreover, if you are in debt of both
. Moreover, if you are in debt of both 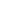 and
and 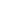 dollars separately, then you are in debt of
dollars separately, then you are in debt of  dollars; therefore,
dollars; therefore, 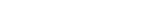 .
.
You can go on and then derive other sets of rules for subtraction, multiplication, and division by using this simple underlying semantics of ![]() and
and ![]() signs: the binary operations
signs: the binary operations ![]() and
and ![]() in an expression like
in an expression like ![]() denote bringing “
denote bringing “![]() number of things” to “
number of things” to “![]() number of things” and taking “
number of things” and taking “![]() number of things from “
number of things from “![]() number of things”, respectively.1 The unary
number of things”, respectively.1 The unary ![]() and
and ![]() operations in expressions like
operations in expressions like ![]() and
and ![]() denote the possession of “
denote the possession of “![]() number of things” and debt of “
number of things” and debt of “![]() number of things”. Now, you can hopefully see how mathematicians can make sense of negative integers as well as the positive ones. It is also worth mentioning that you can switch to other similar, opposing definitions for these operators, and they will still work the same. It is as if the operators and expressions are the interface, and our interpretation of them is the implementation. This may sound very strange since we usually tend to think that whatever we experience in life is the essential part of what is “real”, and mathematics is the actualization of our observations. Here we see the opposite: mathematics is the essential part of what is real, and our observations are the actualization of mathematics.
number of things”. Now, you can hopefully see how mathematicians can make sense of negative integers as well as the positive ones. It is also worth mentioning that you can switch to other similar, opposing definitions for these operators, and they will still work the same. It is as if the operators and expressions are the interface, and our interpretation of them is the implementation. This may sound very strange since we usually tend to think that whatever we experience in life is the essential part of what is “real”, and mathematics is the actualization of our observations. Here we see the opposite: mathematics is the essential part of what is real, and our observations are the actualization of mathematics.
What do fractions mean? As the natural numbers have been generalized to integers, mathematicians have been able to generalize integers to real numbers. Although there are intermediate types of numbers in between the integers and real numbers, I will avoid them for simplicity for regular non-mathy readers. Once you sit down and understand how fractions work, you will see how everything about them is compatible with everything that came before, i.e., the integers. You can represent natural numbers as integers and still work with them without breaking anything. You can represent integers as fractions and still work with them without breaking anything. You can represent fractions as real numbers and still work with them, and nothing breaks in mathematics. Isn’t it beautiful, moving up on the ladder of abstractions without breaking anything in the lower levels? Yes, it is! What we have seen so far is the following: the truth of the integers, of the fractions, and of the reals came to existence only after we were able to have a coherent semantics for them. This was the first of many concepts in the realm of mathematics whose truth is nothing more than the coherence within the elements of the system.
Generalizing factorials to the Gamma function
How do you find the factorial of a positive integer? You multiply all the natural numbers from 1 up to the number, inclusively. ![]() Can you now guess what the
Can you now guess what the ![]() equals? “Obviously, not defined”, you say? Okay, what is the right way to define it then? Would it be correct to define it to be equal to
equals? “Obviously, not defined”, you say? Okay, what is the right way to define it then? Would it be correct to define it to be equal to ![]() ? “Obviously, no”, you say? Ask yourself why you believe so. You’ll find no good reason, but your inner mumblings. To know whether stating
? “Obviously, no”, you say? Ask yourself why you believe so. You’ll find no good reason, but your inner mumblings. To know whether stating ![]() is the wrong way of defining it, one would need to answer the following question: does this definition lead to any conflicts in the (long-term) implications? If the answer is no, then it is not the wrong way of defining 0!. The only optional question you can ask then is whether it is mathematically convenient or not. In this case, it is convinient to define it like that. I’ll give you several reasons.
is the wrong way of defining it, one would need to answer the following question: does this definition lead to any conflicts in the (long-term) implications? If the answer is no, then it is not the wrong way of defining 0!. The only optional question you can ask then is whether it is mathematically convenient or not. In this case, it is convinient to define it like that. I’ll give you several reasons.
Permuting sets. If you needed to find how many permutations there are in the string “abc”, you would calculate ![]() , which is equal to 6 because there are “abc“, “acb“, “bac“, “bca“, “cab“, and “cba“. Now, how many permutations are there in the empty string “”? It cannot be zero because the empty string itself is the least we have. So, the answer is exactly one, which is the empty string itself. Since we used to relate factorials to the number of permutations of sets, it is mathematically correct and convenient to define
, which is equal to 6 because there are “abc“, “acb“, “bac“, “bca“, “cab“, and “cba“. Now, how many permutations are there in the empty string “”? It cannot be zero because the empty string itself is the least we have. So, the answer is exactly one, which is the empty string itself. Since we used to relate factorials to the number of permutations of sets, it is mathematically correct and convenient to define ![]() as 1. It no longer stands for simply multiplying natural numbers from 1 to
as 1. It no longer stands for simply multiplying natural numbers from 1 to ![]() , but the number of all different permutations of a given set. Regardless, the first definition still holds when the given set is not empty.
, but the number of all different permutations of a given set. Regardless, the first definition still holds when the given set is not empty.
Binomial coefficients. How can we find all the binomial coefficients in ![]() ? It turns out this is equal to the number of occurrences of
? It turns out this is equal to the number of occurrences of ![]() when the expression is expanded, which is related to finding the combinations (i.e., similar to permutations but not the same). The formula for it is given by
when the expression is expanded, which is related to finding the combinations (i.e., similar to permutations but not the same). The formula for it is given by ![]() where
where ![]() is the degree of the polynomial (i.e., 3 in our case) and
is the degree of the polynomial (i.e., 3 in our case) and ![]() is the power of the second term
is the power of the second term ![]() . So, what are the first and the last binomial coefficients in
. So, what are the first and the last binomial coefficients in ![]() ? Well, the first term is
? Well, the first term is ![]() and the last term is
and the last term is ![]() . Therefore, the coefficients must be
. Therefore, the coefficients must be ![]() and
and ![]() , respectively. But wait, how do we calculate
, respectively. But wait, how do we calculate ![]() again? Well, if you expand
again? Well, if you expand ![]() by hand, you will see that the first and last coefficients are both 1s. If you cancel out the
by hand, you will see that the first and last coefficients are both 1s. If you cancel out the ![]() s from the fractions, we end up with
s from the fractions, we end up with ![]() , which needs to be equal to
, which needs to be equal to ![]() . So, it is once again mathematically correct and convenient to define
. So, it is once again mathematically correct and convenient to define ![]() to be equal to
to be equal to ![]() .
.
Now, if I asked you to define ![]() , you would think a bit and realize that our current definition of computing factorials does not comply with
, you would think a bit and realize that our current definition of computing factorials does not comply with ![]() since we don’t know how to construct a set with
since we don’t know how to construct a set with ![]() elements in it… So, you wonder whether there is yet another definition to be found, which reduces to our set-related definition when applied to the positive integers, but captures more numbers inherently. This is also what happened with our set-related definition, i.e., it reduces to the very first definition of
elements in it… So, you wonder whether there is yet another definition to be found, which reduces to our set-related definition when applied to the positive integers, but captures more numbers inherently. This is also what happened with our set-related definition, i.e., it reduces to the very first definition of ![]() when applied to non-empty sets. It turns out there is such a definition:
when applied to non-empty sets. It turns out there is such a definition:
![]()
The equation above represents the gamma function. Interestingly enough, ![]() for all positive integers if you compute the integral for any given positive integer
for all positive integers if you compute the integral for any given positive integer ![]() . Moreover, we can set
. Moreover, we can set ![]() to 0.5 and still compute the integral as usual; the answer is
to 0.5 and still compute the integral as usual; the answer is ![]() . So, once again, it is mathematically correct and convenient to use this new definition of factorial, which involves the integral of the gamma function instead of the number of permutations in a given set. Depending on the values of
. So, once again, it is mathematically correct and convenient to use this new definition of factorial, which involves the integral of the gamma function instead of the number of permutations in a given set. Depending on the values of ![]() , it may reduce to the set-related definition, which may also reduce the very first definition.
, it may reduce to the set-related definition, which may also reduce the very first definition.
Generalizing nested integrals to Fractional integrals
What is the integral of a function? It can be seen as the opposite of the derivative. If the derivative of ![]() is
is ![]() , then the integral of
, then the integral of ![]() is
is ![]() . This is called an antiderivative. Fair enough. Then it can also be seen as the area under the curve of a given function. That is to say,
. This is called an antiderivative. Fair enough. Then it can also be seen as the area under the curve of a given function. That is to say, ![]() , which gives us the area under the curve on interval
, which gives us the area under the curve on interval ![]() . Cool! For simplicity, we can let
. Cool! For simplicity, we can let ![]() denote the integration operator
denote the integration operator ![]() to be able to easily represent multiple nested integrals of an arbitrary degree
to be able to easily represent multiple nested integrals of an arbitrary degree ![]() by writing
by writing ![]() , which is the same as
, which is the same as ![]() . Wait, this can be generalized. Check this out:
. Wait, this can be generalized. Check this out:
![]()
If you take a few minutes and think about the equation above, it may start making more sense. I won’t go into the details of why it holds, so I prefer to leave it for the curious reader as homework. What I would like to note, regardless, is the first term in front of the integral that involves computing the factorial. We have seen this before, and we have seen how factorials can be generalized. So, this is what happens when we replace the first term by the infamous ![]() function:
function:
![]()
Wait, now! What if we plugged a non-integer value for ![]() ? Yes, you guessed it right; it would still be a computable expression. Therefore, that means we just have the equation to compute fractional integrals—multiple nested integrals? No, more than that. It descends to ordinary multiple nested integrals whenever
? Yes, you guessed it right; it would still be a computable expression. Therefore, that means we just have the equation to compute fractional integrals—multiple nested integrals? No, more than that. It descends to ordinary multiple nested integrals whenever ![]() is a positive integer. However, it represents something that is beyond nesting multiple integrals in the classical sense of the words “nesting” and “multiple” because we don’t know what 1.5 nested integrals mean. Once again: fascinating! More importantly, it is coherent with what came before it; in fact, it descends to what came before when necessary. The truth is nothing more than the coherence established within the system.
is a positive integer. However, it represents something that is beyond nesting multiple integrals in the classical sense of the words “nesting” and “multiple” because we don’t know what 1.5 nested integrals mean. Once again: fascinating! More importantly, it is coherent with what came before it; in fact, it descends to what came before when necessary. The truth is nothing more than the coherence established within the system.
From ordinary derivatives to Fractional derivatives
What is the derivative of a function? It was originally defined as the slope of a tangent line to a curve at a given point, calculated as the limit of the difference quotient. In other words, we say ![]() . This is intuitive for smooth functions in calculus, like polynomials or trigonometric functions. However, it does not work for pointy functions, and other non-differentiable functions in the classical sense of the word differentiation. For example, one cannot find the slope of a tangent touching the curve of
. This is intuitive for smooth functions in calculus, like polynomials or trigonometric functions. However, it does not work for pointy functions, and other non-differentiable functions in the classical sense of the word differentiation. For example, one cannot find the slope of a tangent touching the curve of ![]() at
at ![]() because it is too sharp and stabs the tangent line whenever it wants to touch the function. So, people invented the notion of a subderivative to handle this. The subderivative of a convex function like
because it is too sharp and stabs the tangent line whenever it wants to touch the function. So, people invented the notion of a subderivative to handle this. The subderivative of a convex function like ![]() does not need to be the slope of a single tangent line anymore; you can have multiple tangent lines if necessary. In this case, the subderivatives of our pointy function
does not need to be the slope of a single tangent line anymore; you can have multiple tangent lines if necessary. In this case, the subderivatives of our pointy function ![]() at
at ![]() is given by a nonempty closed interval
is given by a nonempty closed interval ![]() , where
, where ![]() and
and ![]() . It works… More importantly, it is coherent with what an ordinary derivative would give us at the differentiable interval of the function.
. It works… More importantly, it is coherent with what an ordinary derivative would give us at the differentiable interval of the function.
What about multi-differentiation? Can we calculate the derivative of a function multiple times? Surely we can. ![]() ,
, ![]() ,
, ![]() are all valid expressions. For simplicity, we can let
are all valid expressions. For simplicity, we can let ![]() denote the differentiation operator
denote the differentiation operator ![]() , and then interpret
, and then interpret ![]() for any positive integer
for any positive integer ![]() simply as
simply as ![]() . Similarly, we can let
. Similarly, we can let ![]() denote the anti-derivative of the
denote the anti-derivative of the ![]() -th degree. We have already seen what multi-integration looks like, so we should be able to “multi-integrate” on an interval
-th degree. We have already seen what multi-integration looks like, so we should be able to “multi-integrate” on an interval ![]() as follows:
as follows:
![]()
![]()
Note that ![]() is a middle point between
is a middle point between ![]() and
and ![]() . Knowing what we already know, we can now try to understand what fractional derivatives mean. Well, one can just come up with a nice trick for this: computing a fractional derivative of degree, say 1.5, can be the same as computing the 2nd-order derivative of the integral of order 0.5. Why did I say “can be the same as”? Because it is coherent with the ordinary view of computing multiple nested derivatives; if one wanted to compute the 2nd-order derivative of a given function, it would be the same as taking the 3rd-order derivative of the integral of the function. In other words,
. Knowing what we already know, we can now try to understand what fractional derivatives mean. Well, one can just come up with a nice trick for this: computing a fractional derivative of degree, say 1.5, can be the same as computing the 2nd-order derivative of the integral of order 0.5. Why did I say “can be the same as”? Because it is coherent with the ordinary view of computing multiple nested derivatives; if one wanted to compute the 2nd-order derivative of a given function, it would be the same as taking the 3rd-order derivative of the integral of the function. In other words, ![]() -th order derivative of the
-th order derivative of the ![]() -th order anti-derivative is the same as the
-th order anti-derivative is the same as the ![]() -th order derivative (or, equivalently, the
-th order derivative (or, equivalently, the ![]() -th order anti-derivative). Let’s use the ceil operator on the fractional order to get what we want:
-th order anti-derivative). Let’s use the ceil operator on the fractional order to get what we want:
![]()
![]()
Mathematicians used fractional integrals in order to define fractional derivatives. More importantly, they did so very coherently. Once again, having consistency in mathematical notations and representations opened the doors to the mathematical truth. One wouldn’t be able to simply decide what is allowed to do and what is forbidden to do in math if it weren’t for deciding whether doing something is in coherence with everything else. Once again, coherence is shown to be more inherent than the notion of (ungrounded) truth.
From Real to the Imaginary
You are given a quadratic equation to solve, and it reads ![]() . So, you quickly visualize a square whose area is equal to 1. Then you realize that the variable
. So, you quickly visualize a square whose area is equal to 1. Then you realize that the variable ![]() , denoting the side of the square, must be 1. You then realize that, if you didn’t use the square analogy,
, denoting the side of the square, must be 1. You then realize that, if you didn’t use the square analogy, ![]() could also have been
could also have been ![]() because squaring it also results in
because squaring it also results in ![]() . You say, the answer is
. You say, the answer is ![]() . What if I gave you the following equation instead:
. What if I gave you the following equation instead: ![]() ? Since there is no such real number whose square gives a negative number (i.e.,
? Since there is no such real number whose square gives a negative number (i.e., ![]() ), you would probably say it has no solution. You would be only partially correct. While it has no solution on
), you would probably say it has no solution. You would be only partially correct. While it has no solution on ![]() , we can still try to assume that the equality holds and then see if this assumption causes any conflicts in math. It turns out that assuming that the
, we can still try to assume that the equality holds and then see if this assumption causes any conflicts in math. It turns out that assuming that the ![]() holds for some
holds for some ![]() , even though there is no such real number, is not contradictory — you cannot use it to derive contradictions in math. Since this assumption does not disrupt the mathematical coherence, we might as well give such an
, even though there is no such real number, is not contradictory — you cannot use it to derive contradictions in math. Since this assumption does not disrupt the mathematical coherence, we might as well give such an ![]() a name. Let’s call it
a name. Let’s call it ![]() , the imaginary number. We already know that it is not a real number, so we might as well come up with another dimension of numbers to locate the imaginary number. Let’s call the complex plane, and now we know that
, the imaginary number. We already know that it is not a real number, so we might as well come up with another dimension of numbers to locate the imaginary number. Let’s call the complex plane, and now we know that ![]() is on the complex plane of numbers. Now, if I asked you to solve
is on the complex plane of numbers. Now, if I asked you to solve ![]() , you wouldn’t need to come up with another imaginary number, but instead just simplify this into the existing assumption as follows:
, you wouldn’t need to come up with another imaginary number, but instead just simplify this into the existing assumption as follows: ![]() , implying
, implying ![]() . At this point, it would be obvious to you that
. At this point, it would be obvious to you that ![]() .
.
Pick me infinite elements
Axiom of Choice. Could you pick one element from each set, given 10 sets? Could you do it given 100 sets? 1000 sets? Obviously, you can, given enough time and energy to move your fingers over the elements of each set. How about one element from each set, given infinite sets? Well, the action of picking an element from a set is a straightforward thing, so you think it should be possible, given enough time and energy as before. At this point, you might wonder what picking elements has to do with mathematical coherence and truth. Well, it is actually one of the fundamental parts of math. It is called the axiom of choice (AC) and is used to prove theorems in set theory, topology, algebra, measure theory, probability, and more. In fact, it is also used to order the elements of a given set. Something as simple as ordering is brought into existence by using the AC. Although it seems very intuitive and something that wouldn’t violate our notion of (physical) reality, it comes with interesting implications. One of the implications is that the set of real numbers can be ordered. Another one is you can pick a ball and end up having 2 balls through breaking apart the ball and carefully putting together its pieces. Since the two complete balls have no extra pieces that the original ball didn’t have, it implies that you can get infinite complete balls from a single complete ball. Yet, this axiom is so fundamental. If you believe in some transcendental notion of “truth”, good luck figuring out whether the axiom of choice is true or false. You have neither infinite time nor energy to actually execute the procedures required to construct the balls. However, if you believe in the notion of coherence, then your notion of truth will be tied to all the things that the coherence brings to you.
Well-ordering. It turns out that the AC is equivalently powerful/necessary as ordering any arbitrary non-empty set, including those with infinite elements. Ordering the set of real numbers never seemed so fundamental to what we do in math. The equivalence between the two concepts means that whatever the AC implies, so does the well-ordering principle. For natural numbers, the principle is intuitive: ordering is rooted in the linear and countable progression of natural numbers. When extended to integers, which include negative whole numbers, the principle should still be reasonably straightforward to grasp. However, for real numbers, things become tricky since we do not have a clear, explicit way of ordering real numbers. The step after ordering the set of real numbers is applying well-ordering to transfinite numbers, representing cardinalities beyond the reals. This comes in handy in set theory and transfinite induction. This is also where the ![]() , the lowest transfinite ordinal number, and
, the lowest transfinite ordinal number, and ![]() , the lowest cardinal number, come into play.
, the lowest cardinal number, come into play.
Coherence is fundamental, Truth is emergent
There are many cases in mathematics where nothing seems to make sense and nothing seems to have any connections to the reality that we live in. Yet, mathematics holds and its even unintuitive statements show up in places such as physics where the only concern is the underlying reality, but nothing. How can a physicist not believe in imaginary numbers and still use them to solve an integral in physics? How can an imaginary number be not real and completely imaginary and still show up in equations explaining how reality works? These are interesting questions that some people either avoid asking or answering when asked. In my opinion, truth, in the rigorous mathematical sense of the word, seems nothing more than what we are left with after establishing a coherent mathematical system. Maybe this is the only meta-truth that does not depend on coherence. I don’t know.
- You can hopefully come up with a “meaninful” definitions for multiplication and division operators on your own. ↩︎